July 27, 2018
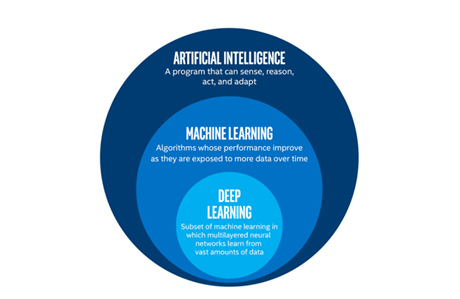
The difference between AI, Machine Learning, and Deep Learning.Not a day goes by without a major news outlet confusing AI, Machine Learning, and Deep Learning The purpose of this article is to break down the differences between AI, Machine Learning, and Deep Learning in layman terms.

July 27, 2018
Get into our very first AI project.Alright so let’s get into our very first AI project. Everyone starts here.